Programs are Proofs
From previous lecture:
fibMono :: n:Nat -> m:{Nat | n < m } -> {fib n <= fib m}
fibMono = fMono fib fibUp
Can we prove any (higher order) logical property?
Logical Properties
Like programming languages, logic has
- syntax (e,∧,∨,¬,⇒,∀,∃),
- meaning (If φ and ψ hold, then φ∧ψ holds), and
- "evaluation" (decision procedures).
Natural Deduction ...
... is a decision procedure for logic.
Propositions <~> Refinement Types
Natural Deduction <~> Lambda Calculus (here Haskell)
This is a Haskell Module!
Motivation
Propositions <~> Refinement Types
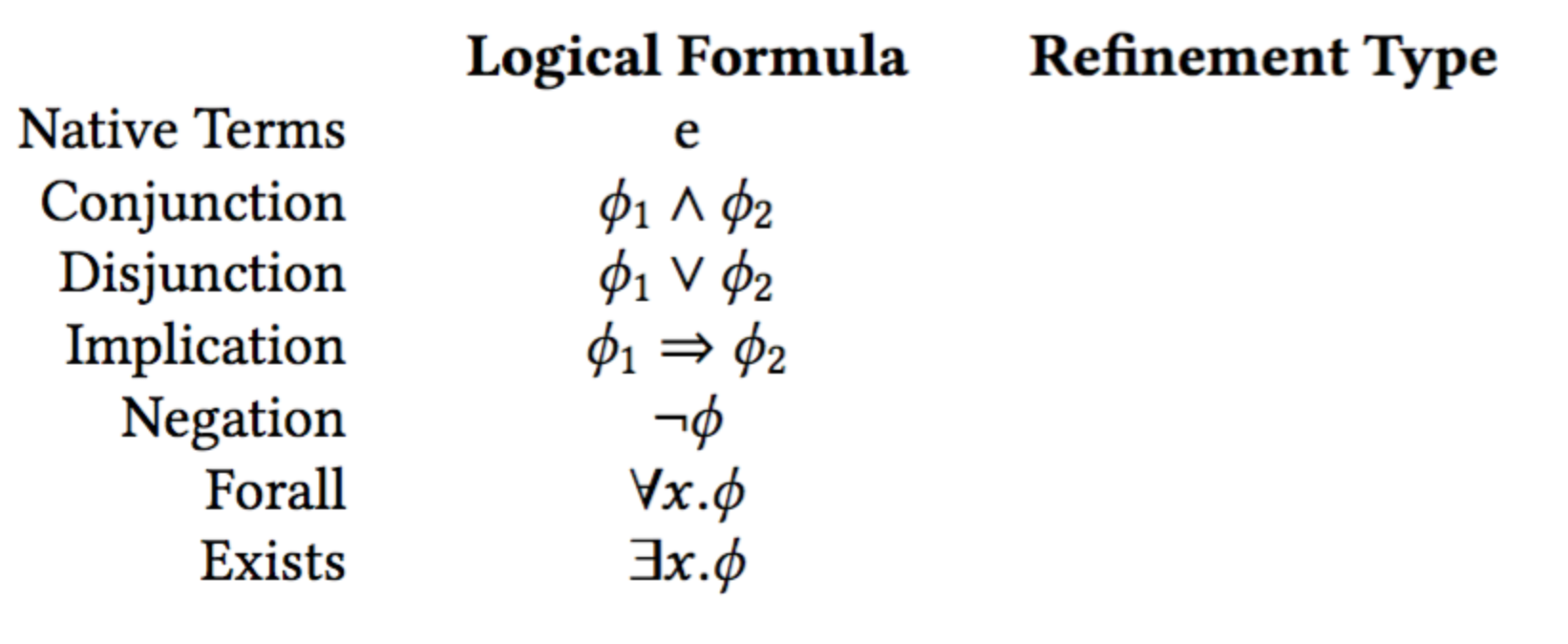
Logic as Types: Native Terms
e <~> {v:() | e}
Propositions <~> Refinement Types
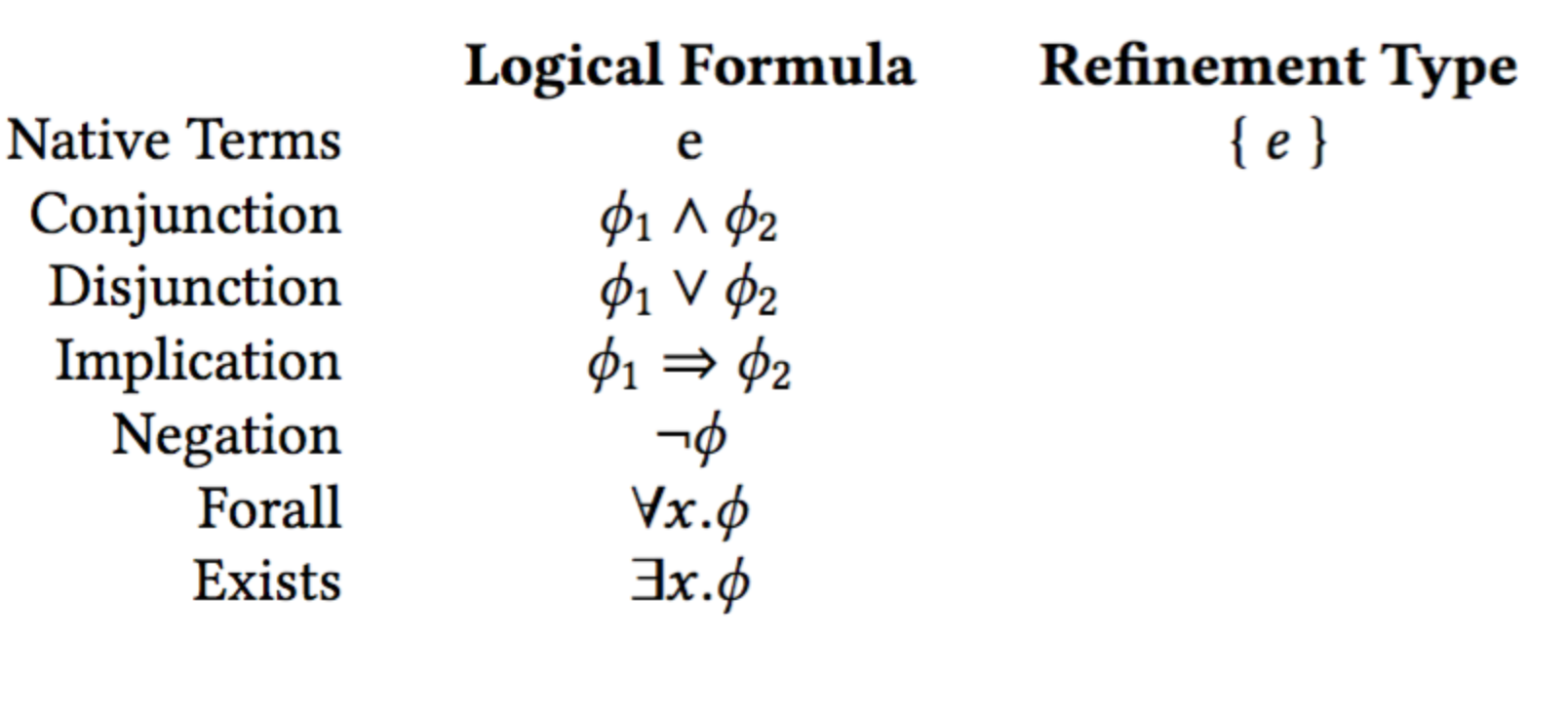
Logic as Types: Conjunction as Pairs
ϕ1 ∧ ϕ2 <~> (ϕ1,ϕ2)
If you know ϕ1 and ϕ2 hold...
then (ϕ1,ϕ2) is a λ-term that shows ϕ1 ∧ ϕ2 holds.
Typing Pairs
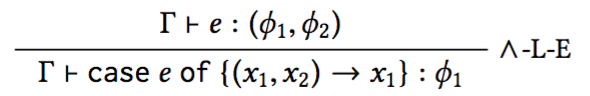
Q: How do we type right?
Typing Pairs
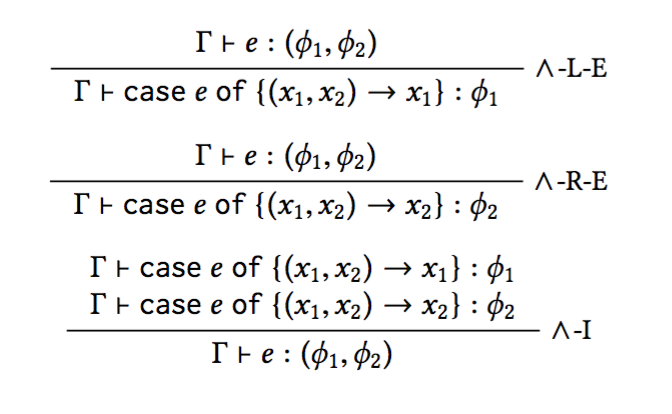
Conjunction <~> Pairs
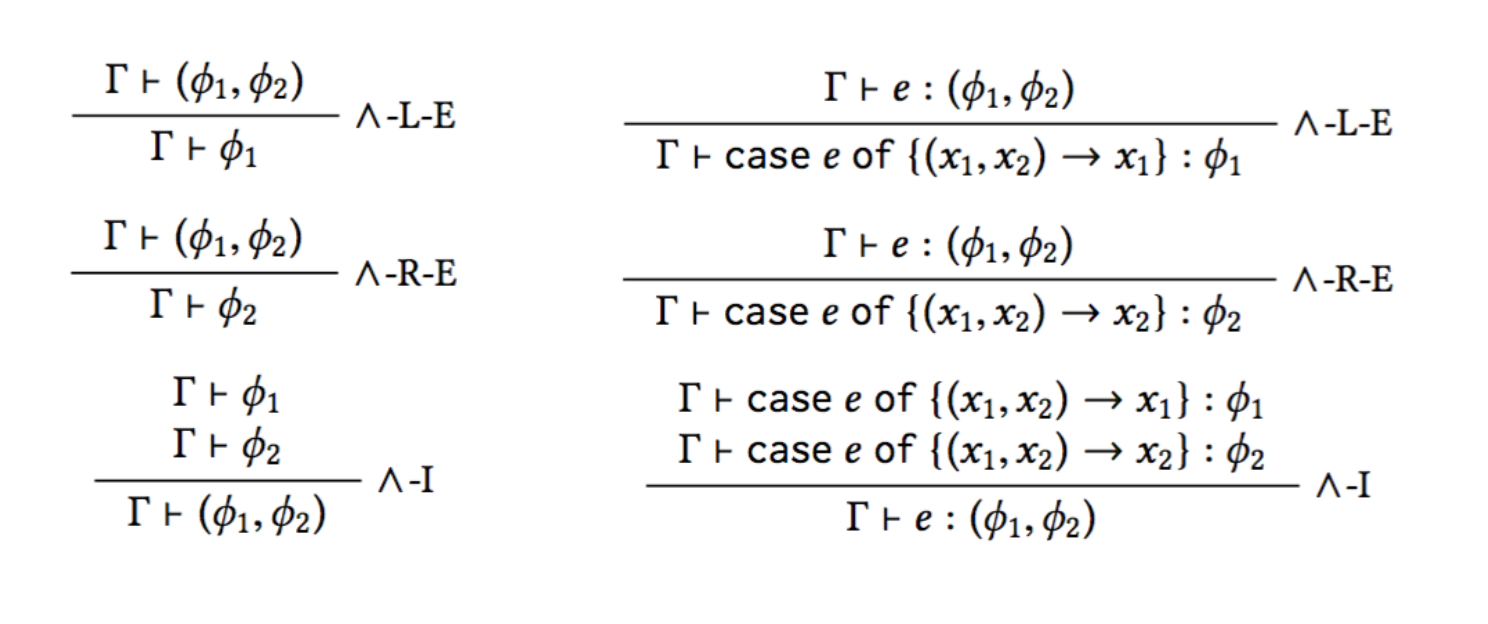
Natural Deduction for Conjunction
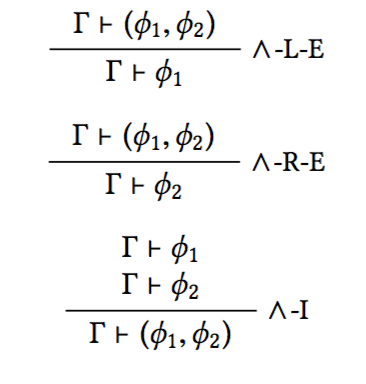
Conjunction Example: Natural Deduction
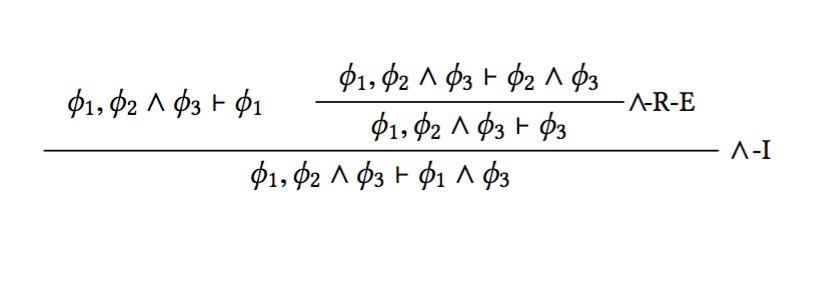
Conjunction Example: Isomorphism
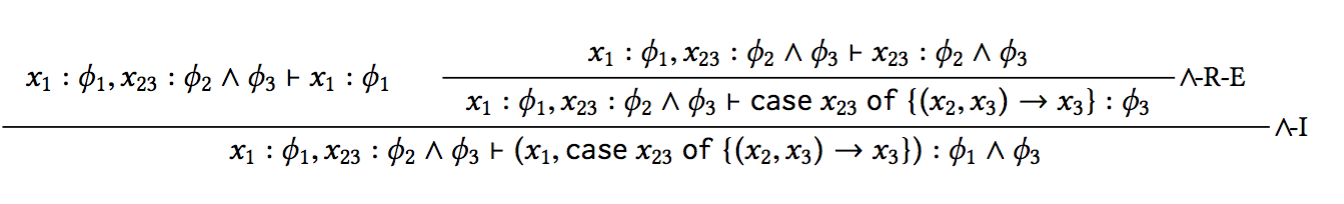
Conjunction Example in Practise
Let's prove: ϕconj ≡ ϕ1, φ2 ∧ ϕ3 |- φ1 ∧ ϕ3
Propositions <~> Refinement Types
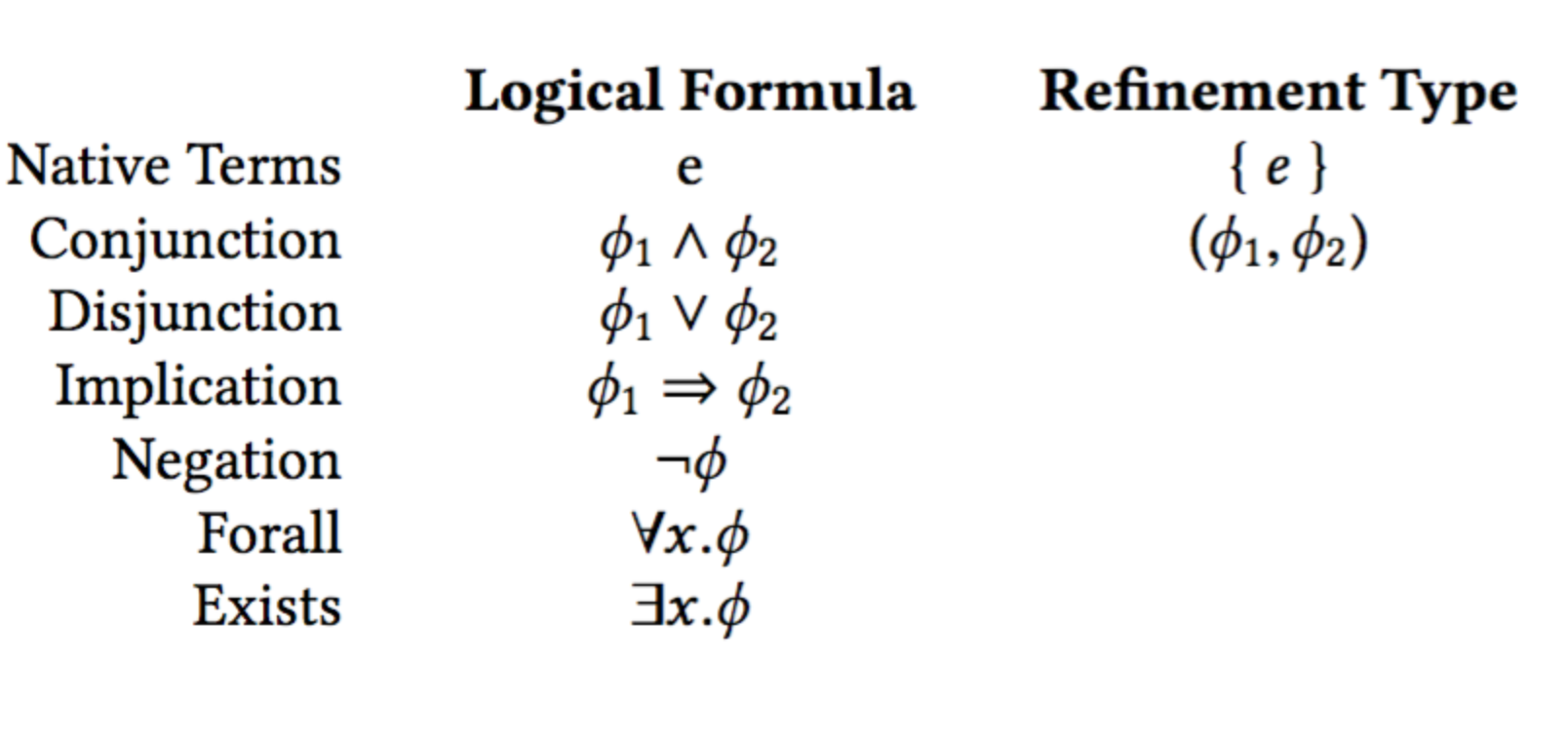
Logic as Types: Disjunction as Either
ϕ1 ∨ ϕ2 <~> Either ϕ1 ϕ2
where data Either a b = Left a | Right b.
If you know ϕ1 or ϕ2 holds...
then Left ϕ1 and Right ϕ2 are λ-terms that shows ϕ1 ∨ ϕ2 holds.
Rules for Disjunction
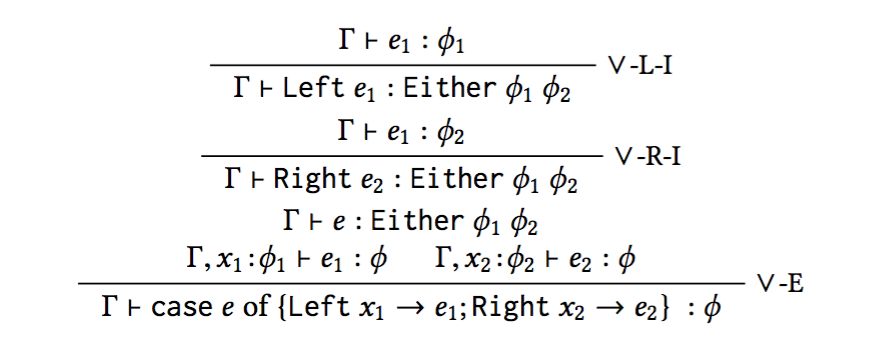
Propositions <~> Refinement Types

Logic as Types: Implication as Function
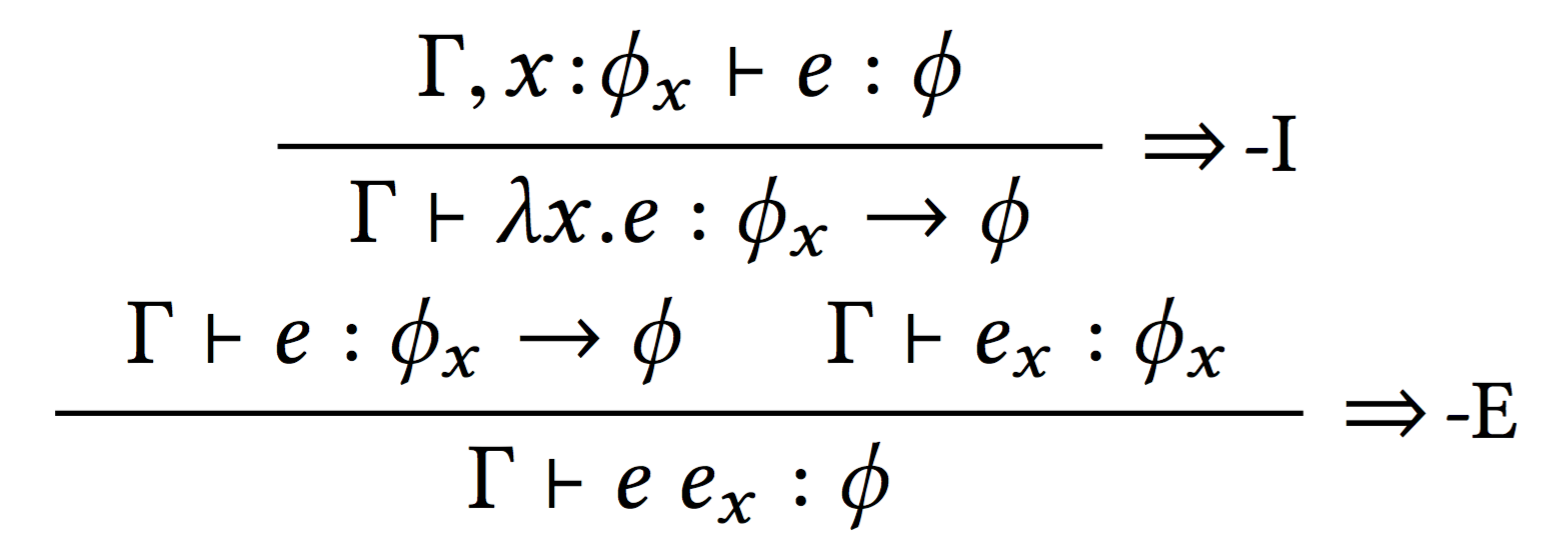
Modus Ponens ...
... is another name for the Implication Elimination Rule.
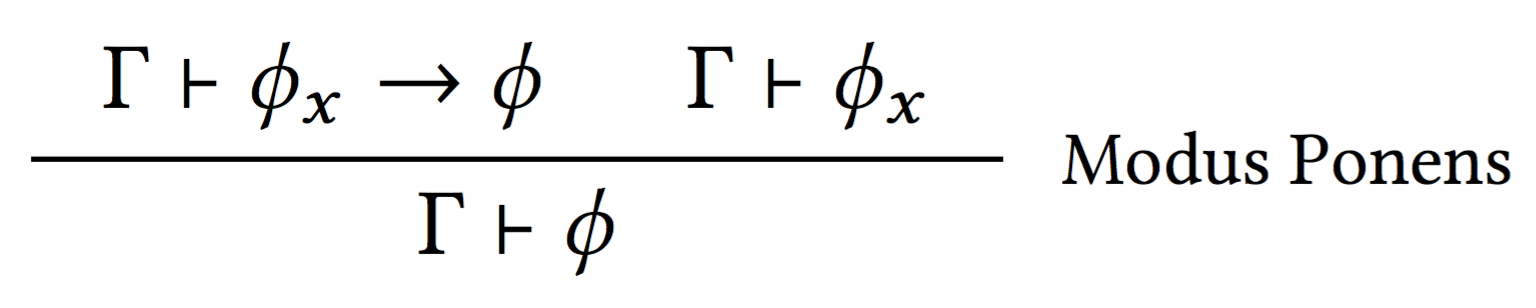
Propositions <~> Refinement Types
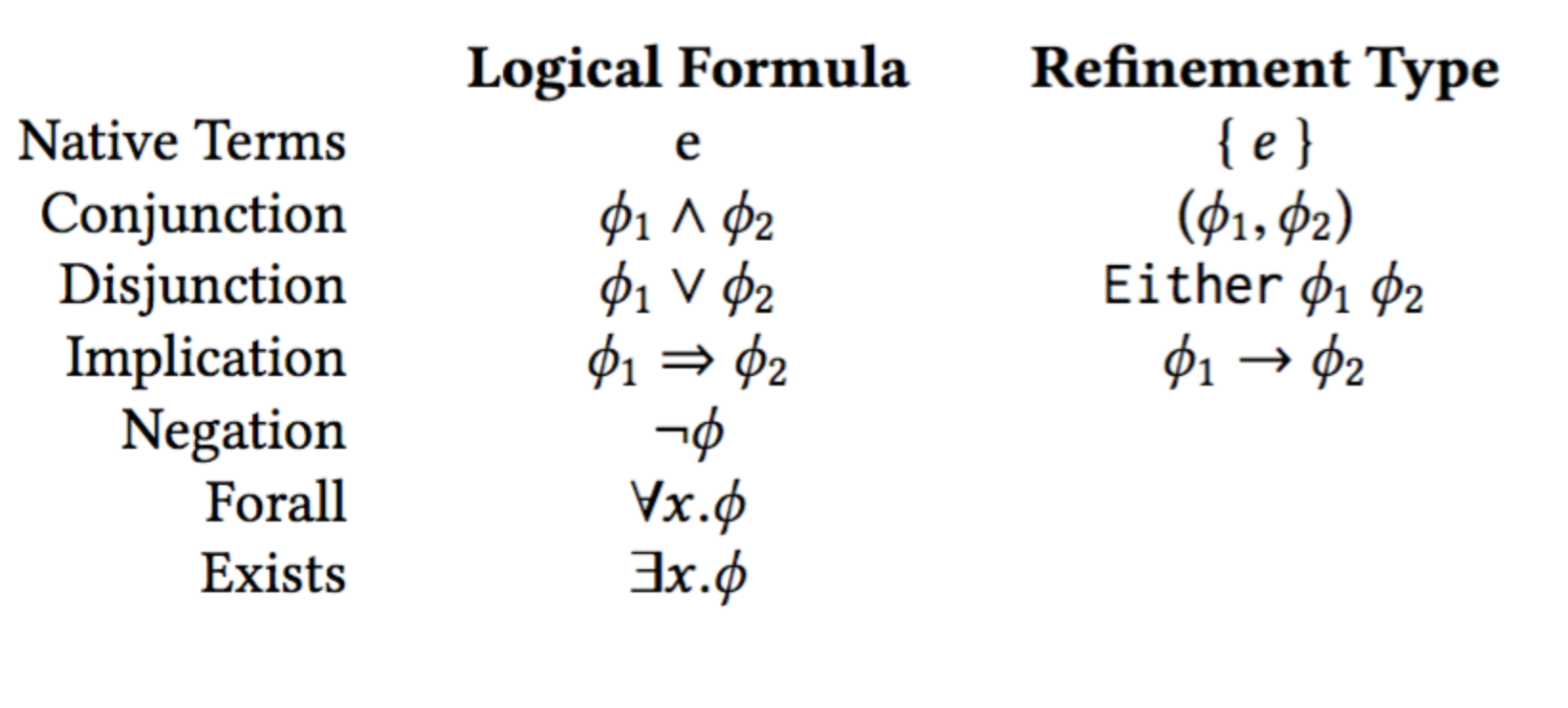
Logic as Types: Negation as Impication
Negetion is just implication to False!
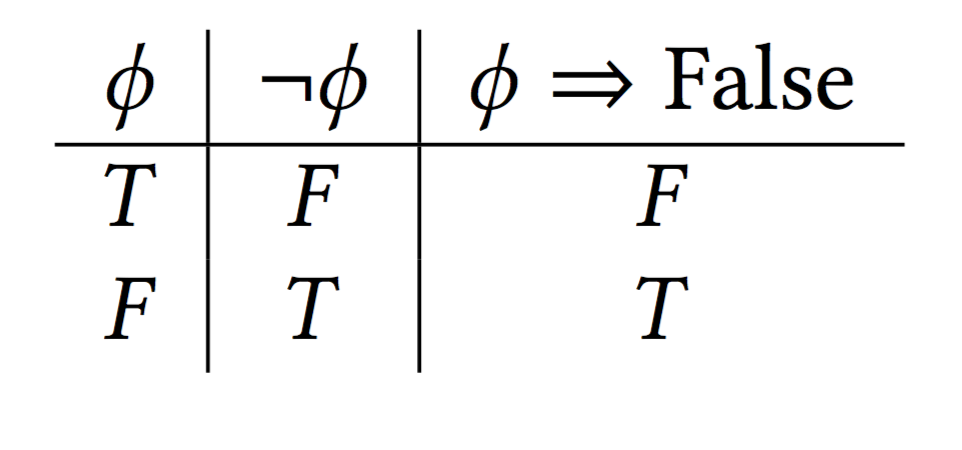
Propositions <~> Refinement Types

Logic as Types: Forall as Function
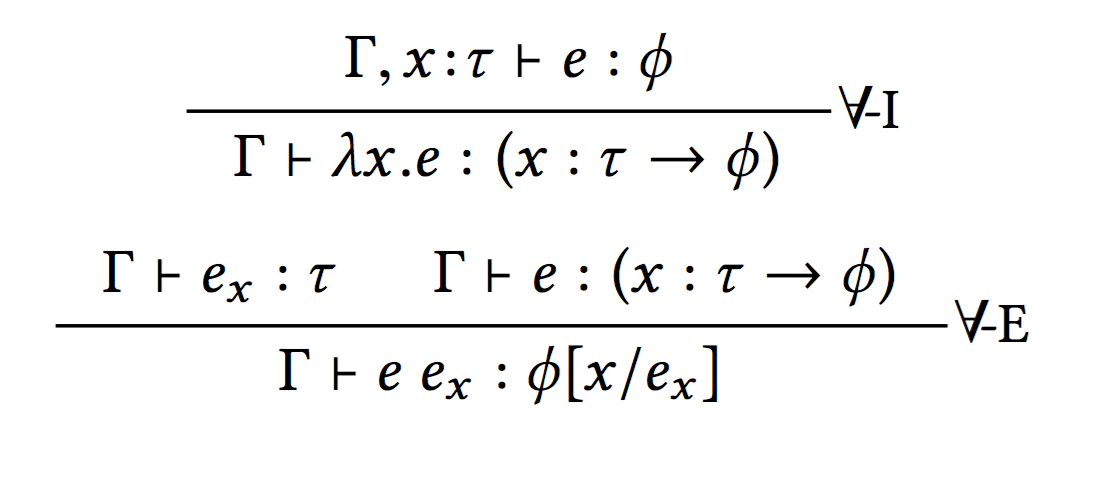
Propositions <~> Refinement Types

Logic as Types: Exists as Pair
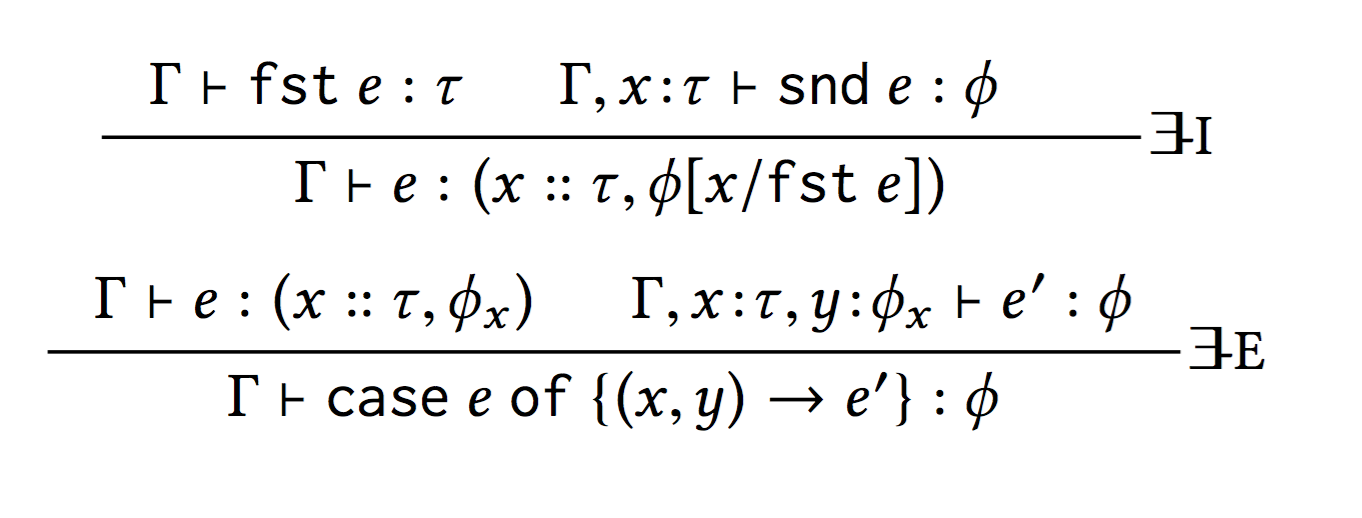
Propositions <~> Refinement Types
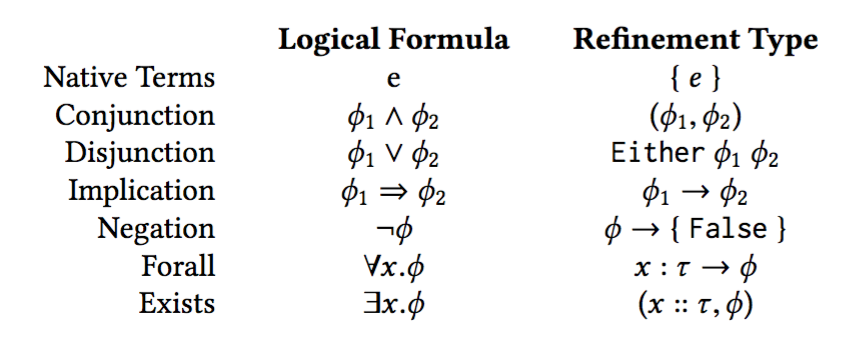
Q: Can you encode the follοwing? ϕ ≡ (∃x.∀y.(p x y)) ⇒ (∀y.∃x.(p x y))
Example existsAll Encoded
Q: Can you define exAll?
Example existsAll in Natural Deduction
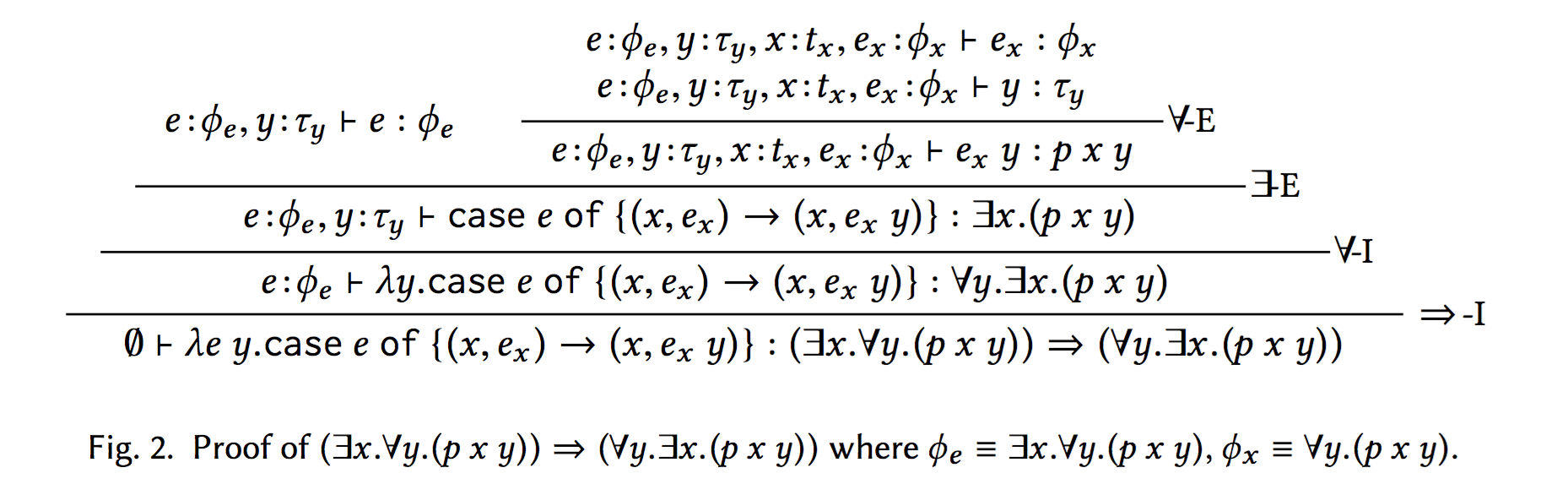
Example II: Distributing Qualifiers
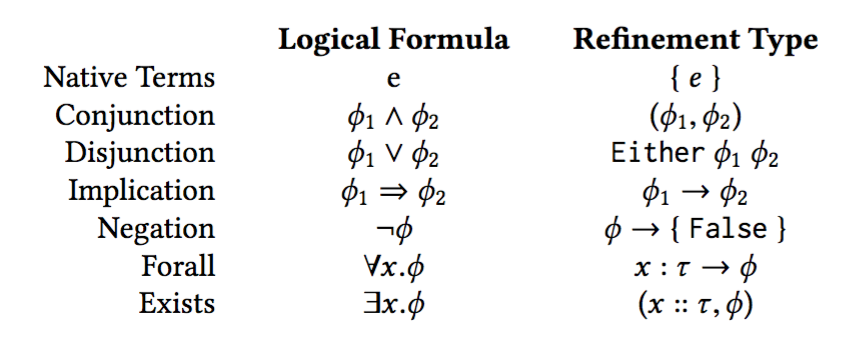
Let's prove: ϕ∃ ≡ (∃x.p x ∨ q x) ⇒ ((∃x.p x) ∨ (∃x.q x))
Example III: Distributing Qualifiers
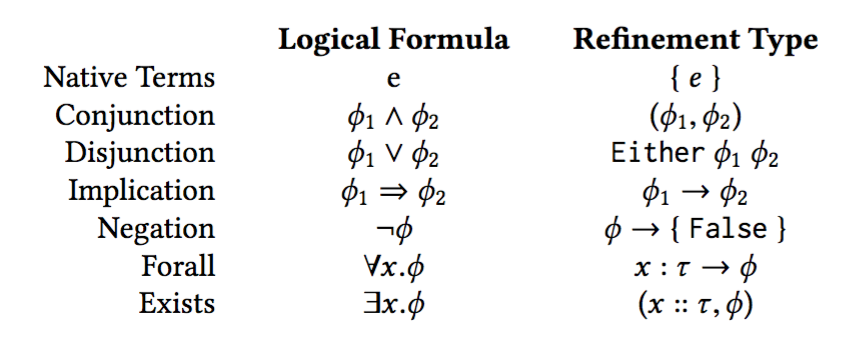
Let's prove: ϕ∀ ≡ (∀x.p x ∧ q x) ⇒ ((∀x.p x) ∧ (∀x.q x))
Example IV: Lists
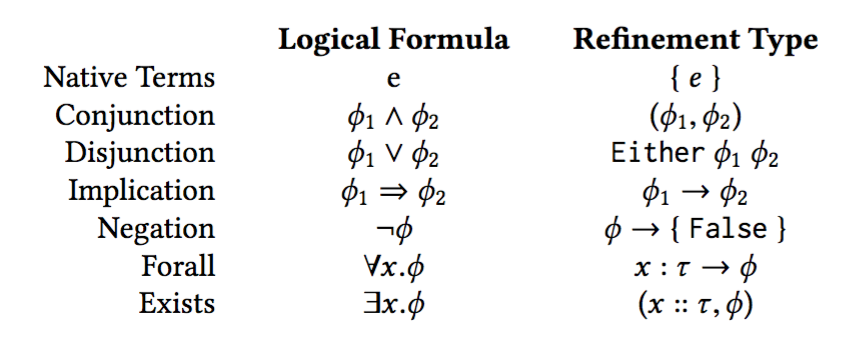
Let's prove: ∀xs.((∃ys. xs = ys ++ ys) ⇒ (∃n.length xs = n + n))
Example V: Natural Induction
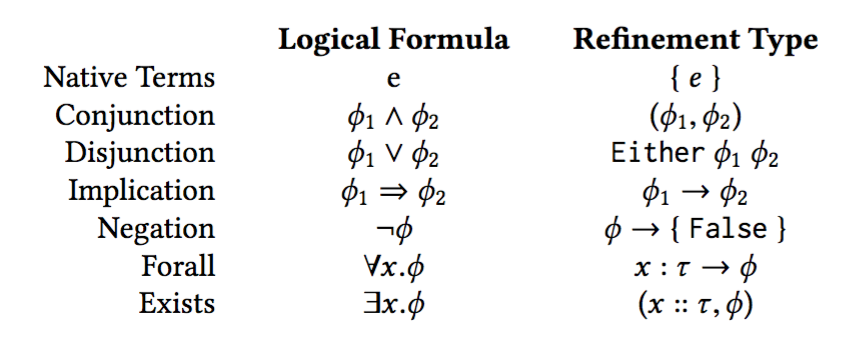
Let's prove: ϕind ≡ (p 0 ∧ (∀n.p (n − 1) ⇒ p n) ⇒ ∀n.p n)
Summing up
Natural Deduction Proofs <~> Lambda Calculus (here Haskell)
Propositions <~> Refinement Types
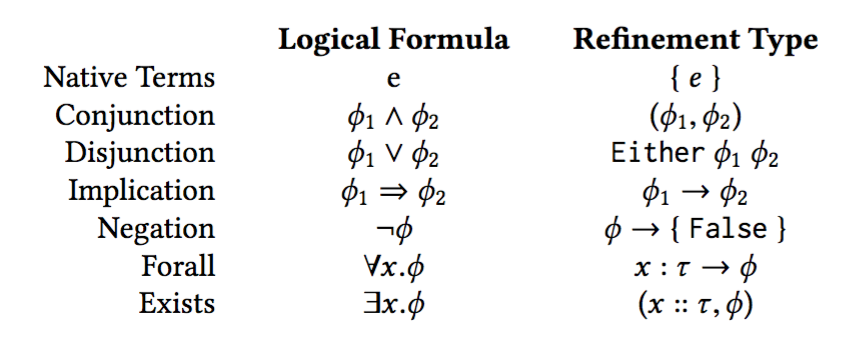
Further Reading:
Propositions as Types, by Wadler & Refinement Reflection, by me et al.