Encoding Natural Deduction


Let's see how natural deduction is encoded as type derivation!

module NaturalDeduction where {-@ LIQUID "--higherorder" @-} {-@ LIQUID "--exact-data-con" @-} import Language.Haskell.Liquid.ProofCombinators import Prelude hiding ((++), length) {-@ infix ++ @-}

Propositions as Types


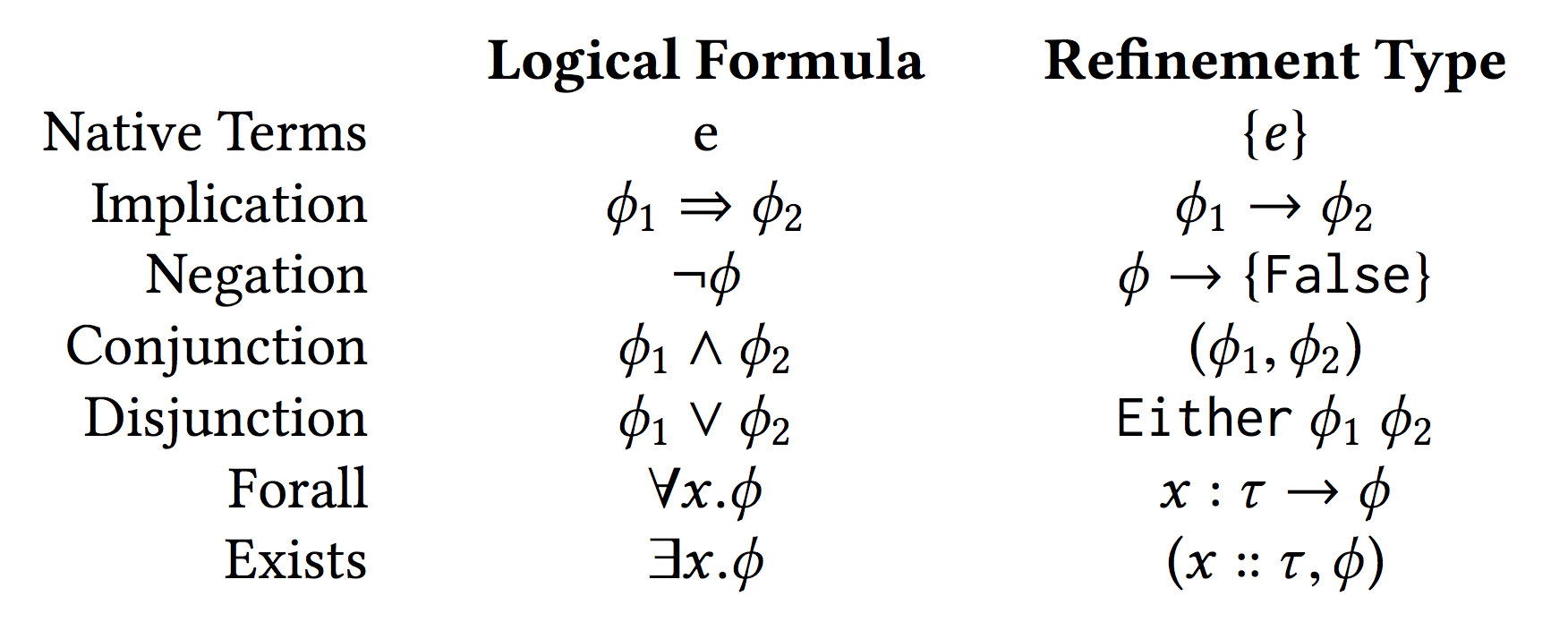
Natural Deduction as Type Derivation


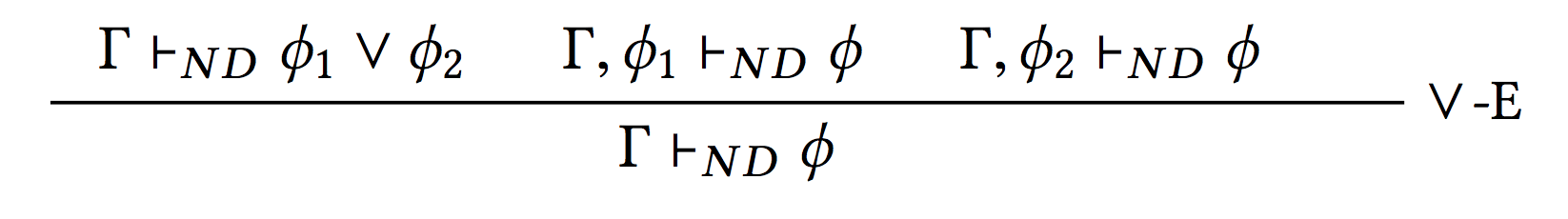
For example, the or-elimination rule

becomes

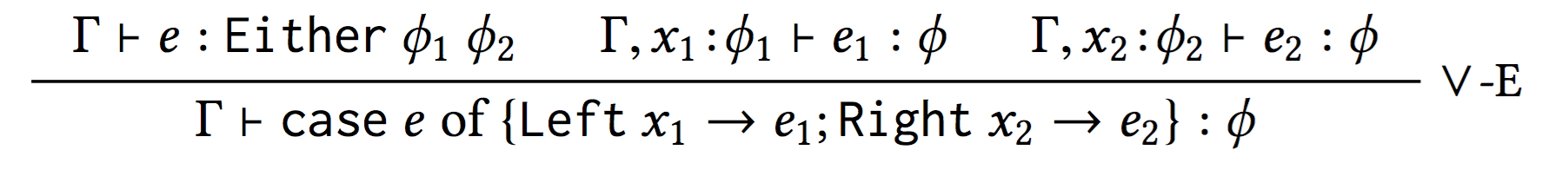
Exists over Forall in Natural Deduction


ϕ ≡ (∃x.∀y.(p x y)) ⇒ (∀y.∃x.(p x y))

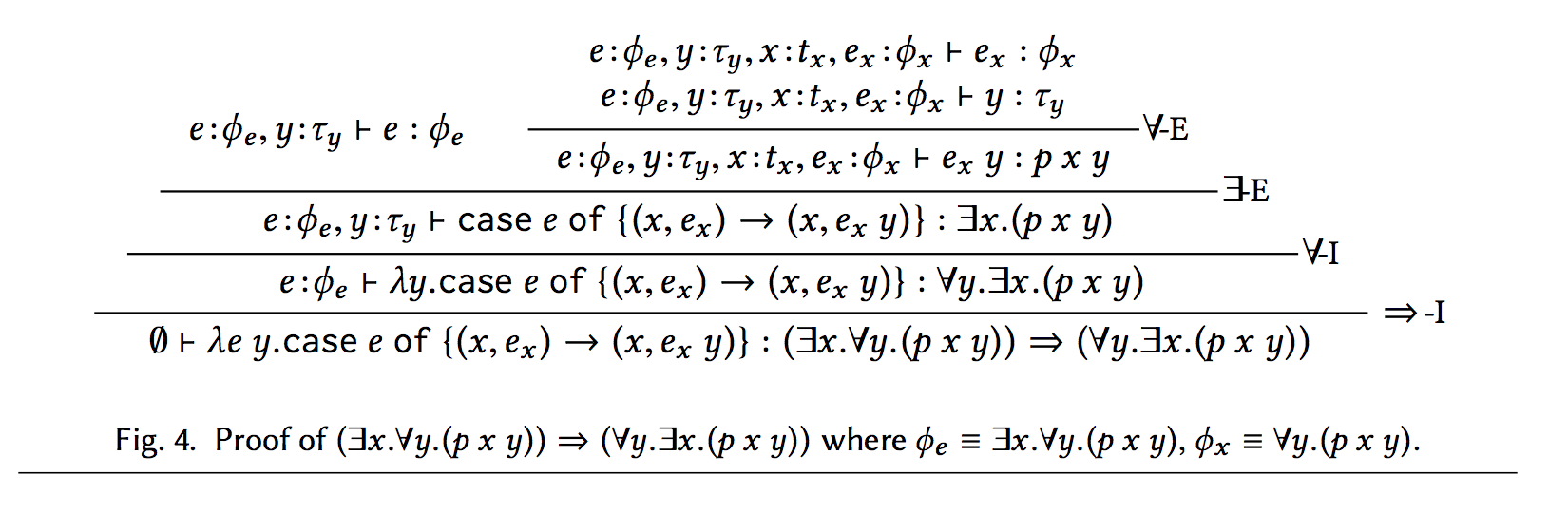
Read bottom up, it is a proof!

Exists over Forall in Natural Deduction


ϕ ≡ (∃x.∀y.(p x y)) ⇒ (∀y.∃x.(p x y))

λe y.case e of {(x, ex ) → (x, ex y)}

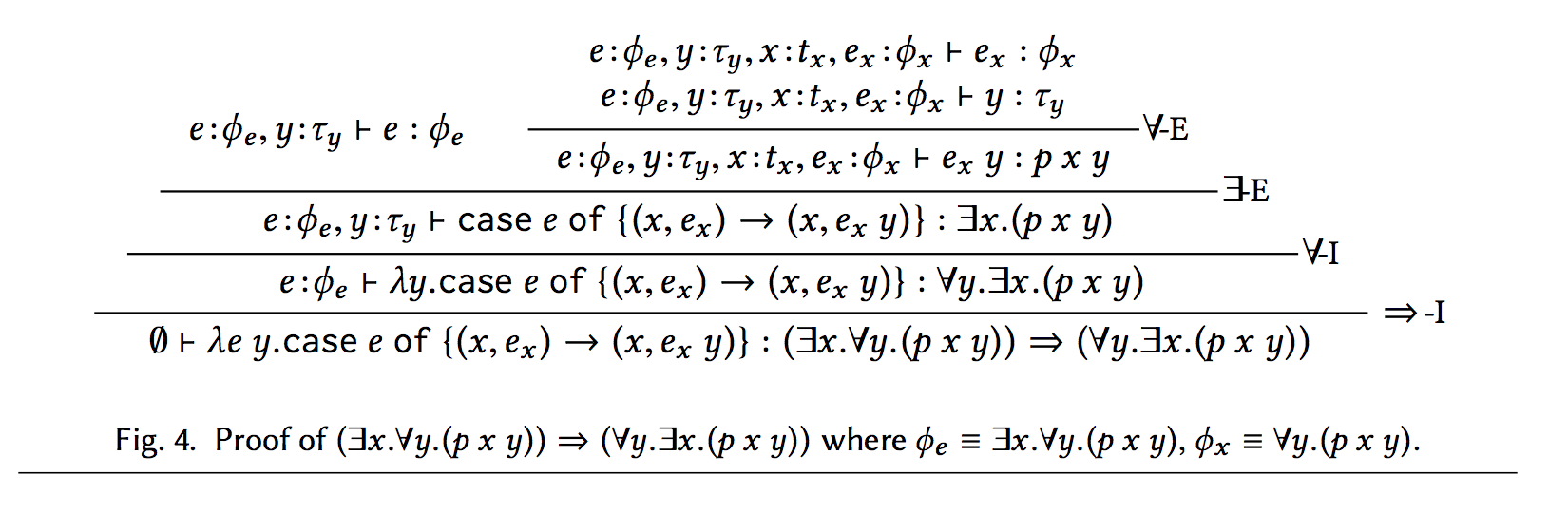
Read top down, we get a proof term!

Exists over Forall in Haskell!


ϕ ≡ (∃x.∀y.(p x y)) ⇒ (∀y.∃x.(p x y))

λe y.case e of {(x, ex ) → (x, ex y)}


{-@ exAll :: p:(a -> a -> Bool) -> (x::a, y:a -> {v:Proof | p x y}) -> y:a -> (x::a, {v:Proof | p x y}) @-} exAll p = \e y -> case e of {(x, ex) -> (x, ex y)}

Distributing Existentials


ϕ∃ ≡ (∃x.p x ∨ q x) ⇒ ((∃x.p x) ∨ (∃x.q x))


{-@ exDistOr :: p : _ -> q : _ -> (x :: a ,Either {v:b | p x } {v:c | q x }) -> Either (x::a , {v:b | p x }) (x::a , {v:c | q x }) @-} exDistOr _ _ (x, Left px) = Left (x, px) exDistOr _ _ (x, Right qx) = Right (x, qx)

Distributing Universals


ϕ∀ ≡ (∀x.p x ∧ q x) ⇒ ((∀x.p x) ∧ (∀x.q x))

{-@ allDistAnd :: p:_ -> q:_ -> (x:a -> ({v:Bool | p x }, {v:Bool| q x})) -> ((x:a -> {v:Bool | p x }), (x:a -> {v:Bool| q x })) @-} allDistAnd _ _ andx = ((\x -> case andx x of (px, _ ) -> px) ,(\x -> case andx x of (_ , qx) -> qx))

Let's use SMT to simplify the proof!

Properties of User Defined Datatypes


ϕ ≡ ∀xs.((∃ys. xs = ys ++ ys) ⇒ (∃n.length xs = n + n))


{-@ evenLen :: xs:_ -> (ys::L a, {v:Proof | xs = ys ++ ys }) -> (n ::Int, {v:Proof | length xs = n + n }) @-} evenLen xs (ys, pf) = (length ys, lenAppend ys ys &&& pf )
where
{-@ lenAppend :: xs:_ -> ys:_ -> { length (xs ++ ys) = length xs + length ys } @-}

Induction on Natural Numbers


ϕind ≡ (p 0 ∧ (∀n.p (n − 1) ⇒ p n) ⇒ ∀n.p n)


{-@ ind :: p:_ -> ({v:Proof| p 0}, (n:Nat -> {v:Proof | p (n-1)} -> {v:Proof | p n})) -> n:Nat -> {v:Proof | p n} @-} ind p (p0, pn) n | n == 0 = p0 | otherwise = pn n (ind p (p0, pn) (n-1))

Summary:


  • Refinement Reflection and Proof by Logical Evaluation combined ...

  • ... allow for complete verification with SMT-automation!


  • Case Study: MapReduce Equivalence
  • Case Study: Encoding Natural Deduction

Haskell Sigs

exDistOr :: (a -> Bool) -> (a -> Bool) -> (a, Either c d) -> Either (a, c) (a,d) exAll :: (a -> a -> Bool) -> (a, a -> Proof) -> a -> (a, Proof) ind :: (Int -> Bool) -> (Proof, Int -> Proof -> Proof) -> Int -> Proof allDistAnd :: (a -> Bool) -> (a -> Bool) -> (a -> (Bool,Bool)) -> (a -> Bool, a -> Bool) evenLen :: L a -> (L a, Proof) -> (Int, Proof)

Code for Lists

{-@ LIQUID "--automatic-instances=liquidinstances" @-} lenAppend :: L a -> L a -> Proof lenAppend N _ = trivial lenAppend (C x xs) ys = lenAppend xs ys
data L a = N | C a (L a) {-@ data L [length] a = N | C {hd :: a, tl :: L a} @-} length :: L a -> Int {-@ length :: x:L a -> {v:Nat | v == length x} @-} {-@ measure length @-} length N = 0 length (C _ xs) = 1 + length xs
The appending function (++) is Haskell's usual append reflected in the logic.
{-@ reflect ++ @-} N ++ ys = ys (C x xs) ++ ys = C x (xs ++ ys)