Measuring Data Types
11: module Measures where 12: import Prelude hiding ((!!), length) 13: import Language.Haskell.Liquid.Prelude 14: 15: length :: L a -> Int 16: (!) :: L a -> Int -> a 17: insert :: Ord a => a -> L a -> L a 18: insertSort :: Ord a => [a] -> L a 19: 20: infixr `C`
Measuring Data Types
Recap
- Refinements: Types + Predicates
- Subtyping: SMT Implication
Example: Length of a List
Given a type for lists:
44: data L a = N | C a (L a)
We can define the length as:
55: {-@ measure llen :: (L a) -> Int 56: llen (N) = 0 57: llen (C x xs) = 1 + (llen xs) @-}
Example: Length of a List
66: {-@ measure llen :: (L a) -> Int 67: llen (N) = 0 68: llen (C x xs) = 1 + (llen xs) @-}
We strengthen data constructor types
78: data L a where 79: N :: {v: L a | (llen v) = 0} 80: C :: a -> t:_ -> {v:_| llen v = 1 + llen t}
Measures Are Uninterpreted
87: data L a where 88: N :: {v: L a | (llen v) = 0} 89: C :: a -> t:_ -> {v:_| llen v = 1 + llen t}
llen is an uninterpreted function in SMT logic
Measures Are Uninterpreted
In SMT, uninterpreted function \(f\) obeys congruence axiom:
\[\forall \overline{x}, \overline{y}. \overline{x} = \overline{y} \Rightarrow f(\overline{x}) = f(\overline{y})\]
Other properties of
llen asserted when typing fold & unfold
Crucial for efficient, decidable and predictable verification.
Measures Are Uninterpreted
Other properties of llen asserted when typing fold & unfold
Fold
129: z = C x y -- z :: {v | llen v = 1 + llen y}
Unfold
137: case z of 138: N -> e1 -- z :: {v | llen v = 0} 139: C x y -> e2 -- z :: {v | llen v = 1 + llen y}
Measured Refinements
Now, we can verify:
152: {-@ length :: xs:L a -> (EqLen xs) @-} 153: forall a. x1:(L a) -> {v : Int | (v == (llen x1)) && (v >= 0)}length N = x1:Int# -> {x2 : Int | (x2 == (x1 : int))}0 154: length (C _ xs) = {x2 : Int | (x2 == (1 : int))}1 x1:Int -> x2:Int -> {x4 : Int | (x4 == (x1 + x2))}+ forall a. x1:(L a) -> {v : Int | (v == (llen x1)) && (v >= 0)}length {x2 : (L a) | (x2 == xs)}xs
Where EqLen is a type alias:
164: {-@ type EqLen Xs = {v:Nat | v = (llen Xs)} @-}
List Indexing Redux
We can type list lookup:
175: {-@ (!) :: xs:L a -> (LtLen xs) -> a @-} 176: (C x _) forall a. x1:(L a) -> {v : Int | (v >= 0) && (v < (llen x1))} -> a! 0 = {VV : a | (VV == x)}x 177: (C _ xs) ! i = (L {VV : a | (x <= VV)})xs forall a. x1:(L a) -> {v : Int | (v >= 0) && (v < (llen x1))} -> a! ({x2 : Int | (x2 >= 0)}i x1:Int -> x2:Int -> {x4 : Int | (x4 == (x1 - x2))}- {x2 : Int | (x2 == (1 : int))}1) 178: _ ! _ = {x1 : [Char] | false} -> aliquidError {x2 : [Char] | ((len x2) >= 0)}"never happens!"
Where LtLen is a type alias:
187: {-@ type LtLen Xs = {v:Nat | v < (llen Xs)} @-}
Demo: What if we remove the precondition?
Multiple Measures
Support many measures on a type ...
... by conjoining the constructor refinements.
Multiple Measures: Red-Black Trees
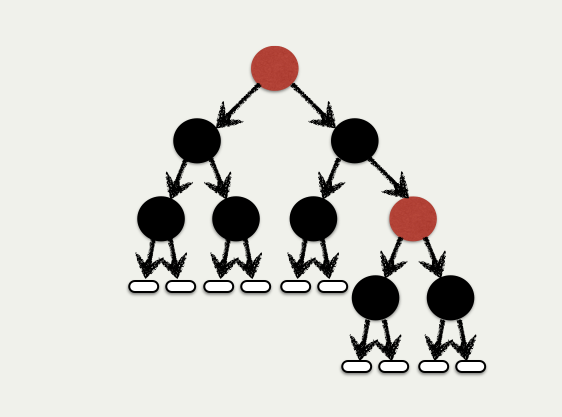
- Color:
Rednodes haveBlackchildren - Height: Number of
Blacknodes equal on all paths
Basic Type
282: data Tree a = Leaf 283: | Node Color a (Tree a) (Tree a) 284: 285: data Color = Red 286: | Black
Color Invariant
Red nodes have Black children
296: measure isRB :: Tree a -> Prop 297: isRB (Leaf) = true 298: isRB (Node c x l r) = c=Red => (isB l && isB r) 299: && isRB l && isRB r
where
305: measure isB :: Tree a -> Prop 306: isB (Leaf) = true 307: isB (Node c x l r) = c == Black
Almost Color Invariant
Color Invariant except at root.
322: measure isAlmost :: Tree a -> Prop 323: isAlmost (Leaf) = true 324: isAlmost (Node c x l r) = isRB l && isRB r
Height Invariant
Number of Black nodes equal on all paths
336: measure isBH :: RBTree a -> Prop 337: isBH (Leaf) = true 338: isBH (Node c x l r) = bh l = bh r 339: && isBH l && isBH r
where
345: measure bh :: RBTree a -> Int 346: bh (Leaf) = 0 347: bh (Node c x l r) = bh l 348: + if c = Red then 0 else 1
Refined Type
356: -- Red-Black Trees 357: type RBT a = {v:Tree a | isRB v && isBH v} 358: 359: -- Almost Red-Black Trees 360: type ARBT a = {v:Tree a | isAlmost v && isBH v}
Refined Data Constructors
Can encode invariants inside constructors
408: {-@ data L a = N 409: | C { x :: a 410: , xs :: L {v:a| x <= v} } @-}
Head
x is less than every element of tail xs
i.e. specifies increasing Lists
Increasing Lists
429: data L a where 430: N :: L a 431: C :: x:a -> xs: L {v:a | x <= v} -> L a
- We check property when folding
C - We assume property when unfolding
C
Increasing Lists
Demo: Insertion Sort (hover for inferred types)
447: forall a. (Ord a) => [a] -> (L a)insertSort = (a -> (L a) -> (L a)) -> (L a) -> [a] -> (L a)foldr a -> (L a) -> (L a)insert {x3 : (L a) | (((isNull x3)) <=> true) && ((llen x3) == 0)}N 448: 449: forall a. (Ord a) => a -> (L a) -> (L a)insert ay (x `C` xs) 450: | {VV : a | (VV == y)}y x1:a -> x2:a -> {x2 : Bool | (((Prop x2)) <=> (x1 <= x2))}<= {VV : a | (VV == x)}x = {VV : a | (VV == y)}y x1:a -> x2:(L {VV : a | (x1 <= VV)}) -> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` ({VV : a | (VV == x)}x x1:{VV : a | (VV >= x) && (VV >= y)} -> x2:(L {VV : a | (VV >= x) && (VV >= y) && (x1 <= VV)}) -> {x5 : (L {VV : a | (VV >= x) && (VV >= y)}) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` {x2 : (L {VV : a | (x <= VV)}) | (x2 == xs)}xs) 451: | otherwise = {VV : a | (VV == x)}x x1:a -> x2:(L {VV : a | (x1 <= VV)}) -> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` forall a. (Ord a) => a -> (L a) -> (L a)insert {VV : a | (VV == y)}y {x2 : (L {VV : a | (x <= VV)}) | (x2 == xs)}xs 452: insert y N = {VV : a | (VV == y)}y x1:a -> x2:(L {VV : a | (x1 <= VV)}) -> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` {x3 : (L {VV : a | false}) | (((isNull x3)) <=> true) && ((llen x3) == 0)}N
Problem 1: What if we need increasing & decreasing lists?
Recap
- Refinements: Types + Predicates
- Subtyping: SMT Implication
- Measures: Strengthened Constructors
- Decouple property from structure