Measuring Data Types

11: module Measures where
12: import Prelude hiding ((!!), length)
13: import Language.Haskell.Liquid.Prelude
14: 
15: length      :: L a -> Int
16: (!)         :: L a -> Int -> a
17: insert      :: Ord a => a -> L a -> L a
18: insertSort  :: Ord a => [a] -> L a
19: 
20: infixr `C`

Measuring Data Types

Recap

Refinements: Types + Predicates
Subtyping: SMT Implication

Example: Length of a List

Given a type for lists:

44: data L a = N | C a (L a)

We can define the length as:

55: {-@ measure llen  :: (L a) -> Int
56:     llen (N)      = 0
57:     llen (C x xs) = 1 + (llen xs)  @-}

Example: Length of a List

66: {-@ measure llen  :: (L a) -> Int
67:     llen (N)      = 0
68:     llen (C x xs) = 1 + (llen xs)  @-}

LiquidHaskell strengthens data constructor types

78: data L a where 
79:   N :: {v: L a | (llen v) = 0}
80:   C :: a -> t:_ -> {v:_| llen v = 1 + llen t}

Measures Are Uninterpreted

87: data L a where 
88:   N :: {v: L a | (llen v) = 0}
89:   C :: a -> t:_ -> {v:_| llen v = 1 + llen t}

llen is an uninterpreted function in SMT logic

Measures Are Uninterpreted

In SMT, uninterpreted function f obeys congruence axiom:

forall x y. (x = y) => (f x) = (f y)

All other facts about llen asserted at fold and unfold

Measures Are Uninterpreted

Facts about llen asserted at syntax-directed fold and unfold

Fold

122: z = C x y     -- z :: {v | llen v = 1 + llen y}

Unfold

130: case z of 
131:   N     -> e1 -- z :: {v | llen v = 0}
132:   C x y -> e2 -- z :: {v | llen v = 1 + llen y}

Measured Refinements

Now, we can verify:

145: {-@ length      :: xs:L a -> (EqLen xs) @-}
146: forall a. x1:(L a) -> {v : Int | (v == (llen x1)) && (v >= 0)}length N        = x1:Int# -> {x2 : Int | (x2 == (x1  :  int))}0
147: length (C _ xs) = {x2 : Int | (x2 == (1  :  int))}1 x1:Int -> x2:Int -> {x4 : Int | (x4 == (x1 + x2))}+ forall a. x1:(L a) -> {v : Int | (v == (llen x1)) && (v >= 0)}length {x2 : (L a) | (x2 == xs)}xs

Where EqLen is a type alias:

157: {-@ type EqLen Xs = {v:Nat | v = (llen Xs)} @-}

List Indexing Redux

We can type list lookup:

168: {-@ (!)      :: xs:L a -> (LtLen xs) -> a @-}
169: (C x _)  forall a. x1:(L a) -> {v : Int | (v >= 0) && (v < (llen x1))} -> a! 0 = {VV : a | (VV == x)}x
170: (C _ xs) ! i = (L {VV : a | (x <= VV)})xs forall a. x1:(L a) -> {v : Int | (v >= 0) && (v < (llen x1))} -> a! ({x2 : Int | (x2 >= 0)}i x1:Int -> x2:Int -> {x4 : Int | (x4 == (x1 - x2))}- {x2 : Int | (x2 == (1  :  int))}1)
171: _        ! _ = {x1 : [Char] | false} -> aliquidError {x2 : [Char] | ((len x2) >= 0)}"never happens!"

Where LtLen is a type alias:

180: {-@ type LtLen Xs = {v:Nat | v < (llen Xs)} @-}

Demo: What if we remove the precondition?

Multiple Measures

LiquidHaskell allows many measures for a type

Ex: List Emptiness

Measure describing whether a List is empty

205: {-@ measure isNull :: (L a) -> Prop
206:     isNull (N)      = true
207:     isNull (C x xs) = false           @-}

LiquidHaskell strengthens data constructors

216: data L a where 
217:   N :: {v : L a | (isNull v)}
218:   C :: a -> L a -> {v:(L a) | not (isNull v)}

Conjoining Refinements

Data constructor refinements are conjoined

229: data L a where 
230:   N :: {v:L a |  (llen v) = 0 
231:               && (isNull v) }
232:   C :: a 
233:     -> xs:L a 
234:     -> {v:L a |  (llen v) = 1 + (llen xs) 
235:               && not (isNull v)          }

Multiple Measures: Red-Black Trees

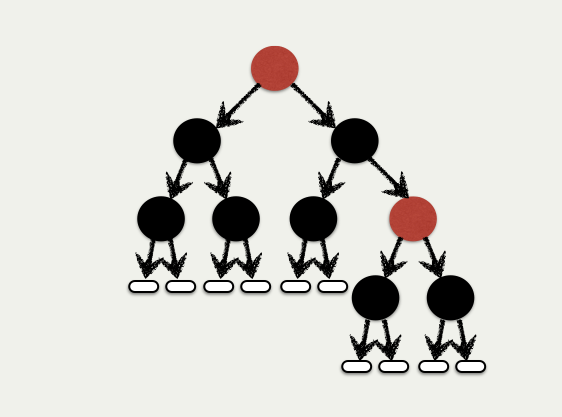
Color Invariant: Red nodes have Black children
Height Invariant: Number of Black nodes equal on all paths

[Skip...]

Basic Type

256: data Tree a = Leaf 
257:             | Node Color a (Tree a) (Tree a)
258: 
259: data Color  = Red 
260:             | Black

Color Invariant

Red nodes have Black children

270: measure isRB        :: Tree a -> Prop
271: isRB (Leaf)         = true
272: isRB (Node c x l r) = c=Red => (isB l && isB r)
273:                       && isRB l && isRB r

where

279: measure isB         :: Tree a -> Prop 
280: isB (Leaf)          = true
281: isB (Node c x l r)  = c == Black

Almost Color Invariant

Color Invariant except at root.

296: measure isAlmost        :: Tree a -> Prop
297: isAlmost (Leaf)         = true
298: isAlmost (Node c x l r) = isRB l && isRB r

Height Invariant

Number of Black nodes equal on all paths

310: measure isBH        :: RBTree a -> Prop
311: isBH (Leaf)         =  true
312: isBH (Node c x l r) =  bh l = bh r 
313:                     && isBH l && isBH r

where

319: measure bh        :: RBTree a -> Int
320: bh (Leaf)         = 0
321: bh (Node c x l r) = bh l 
322:                   + if c = Red then 0 else 1

Refined Type

330: -- Red-Black Trees
331: type RBT a  = {v:Tree a | isRB v && isBH v}
332: 
333: -- Almost Red-Black Trees
334: type ARBT a = {v:Tree a | isAlmost v && isBH v}

Details

Measures vs. Index Types

Decouple Property & Type

Unlike indexed types ...

Measures decouple properties from structures
Support multiple properties over structures
Enable reuse of structures in different contexts

Invaluable in practice!

Refined Data Constructors

Can encode invariants inside constructors

379: {-@ data L a = N
380:              | C { x  :: a 
381:                  , xs :: L {v:a| x <= v} } @-}

Head x is less than every element of tail xs

i.e. specifies increasing Lists

Increasing Lists

400: data L a where
401:   N :: L a
402:   C :: x:a -> xs: L {v:a | x <= v} -> L a

LiquidHaskell checks property when folding C
LiquidHaskell assumes property when unfolding C

Increasing Lists

Demo: Insertion Sort (hover for inferred types)

418: forall a. (Ord a) => [a] -> (L a)insertSort = (a -> (L a) -> (L a)) -> (L a) -> [a] -> (L a)foldr a -> (L a) -> (L a)insert {x3 : (L a) | (((isNull x3)) <=> true) && ((llen x3) == 0)}N
419: 
420: forall a. (Ord a) => a -> (L a) -> (L a)insert ay (x `C` xs) 
421:   | {VV : a | (VV == y)}y x1:a -> x2:a -> {x2 : Bool | (((Prop x2)) <=> (x1 <= x2))}<= {VV : a | (VV == x)}x    = {VV : a | (VV == y)}y x1:a
-> x2:(L {VV : a | (x1 <= VV)})
-> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` ({VV : a | (VV == x)}x x1:{VV : a | (VV >= x) && (VV >= y)}
-> x2:(L {VV : a | (VV >= x) && (VV >= y) && (x1 <= VV)})
-> {x5 : (L {VV : a | (VV >= x) && (VV >= y)}) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` {x2 : (L {VV : a | (x <= VV)}) | (x2 == xs)}xs)
422:   | otherwise = {VV : a | (VV == x)}x x1:a
-> x2:(L {VV : a | (x1 <= VV)})
-> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` forall a. (Ord a) => a -> (L a) -> (L a)insert {VV : a | (VV == y)}y {x2 : (L {VV : a | (x <= VV)}) | (x2 == xs)}xs
423: insert y N    = {VV : a | (VV == y)}y x1:a
-> x2:(L {VV : a | (x1 <= VV)})
-> {x5 : (L a) | (((isNull x5)) <=> false) && ((llen x5) == (1 + (llen x2))) && ((x1 x5) == x1) && ((x2 x5) == x2)}`C` {x3 : (L {VV : a | false}) | (((isNull x3)) <=> true) && ((llen x3) == 0)}N

Problem 1: What if we need both increasing and decreasing lists?

Recap

Refinements: Types + Predicates
Subtyping: SMT Implication
Measures: Strengthened Constructors
- Decouple property from structure
- Reuse structure across different properties

[continue]