What is PeaCoq?

Over the past year, I have developed a Coq frontend called PeaCoq (not to be mistaken with Yves Bertot’s Pcoq). If you wish to play with it before or while reading this article, I made an online version available here. Note that it will reset after 15 minutes of inactivity, and that it might go down any time!

There have been several attempts at improving user interfaces for proof assistants, so I will describe here some of PeaCoq’s features. I built PeaCoq with the goal of helping both novice and more advanced users. I chose to build it as a web-based text editor, so that it was easy to have people try it. The client-server architecture means PeaCoq users only need a web browser to interact with a Coq session hosted on the server. Unfortunately, this means PeaCoq does not run in your favorite text editor.

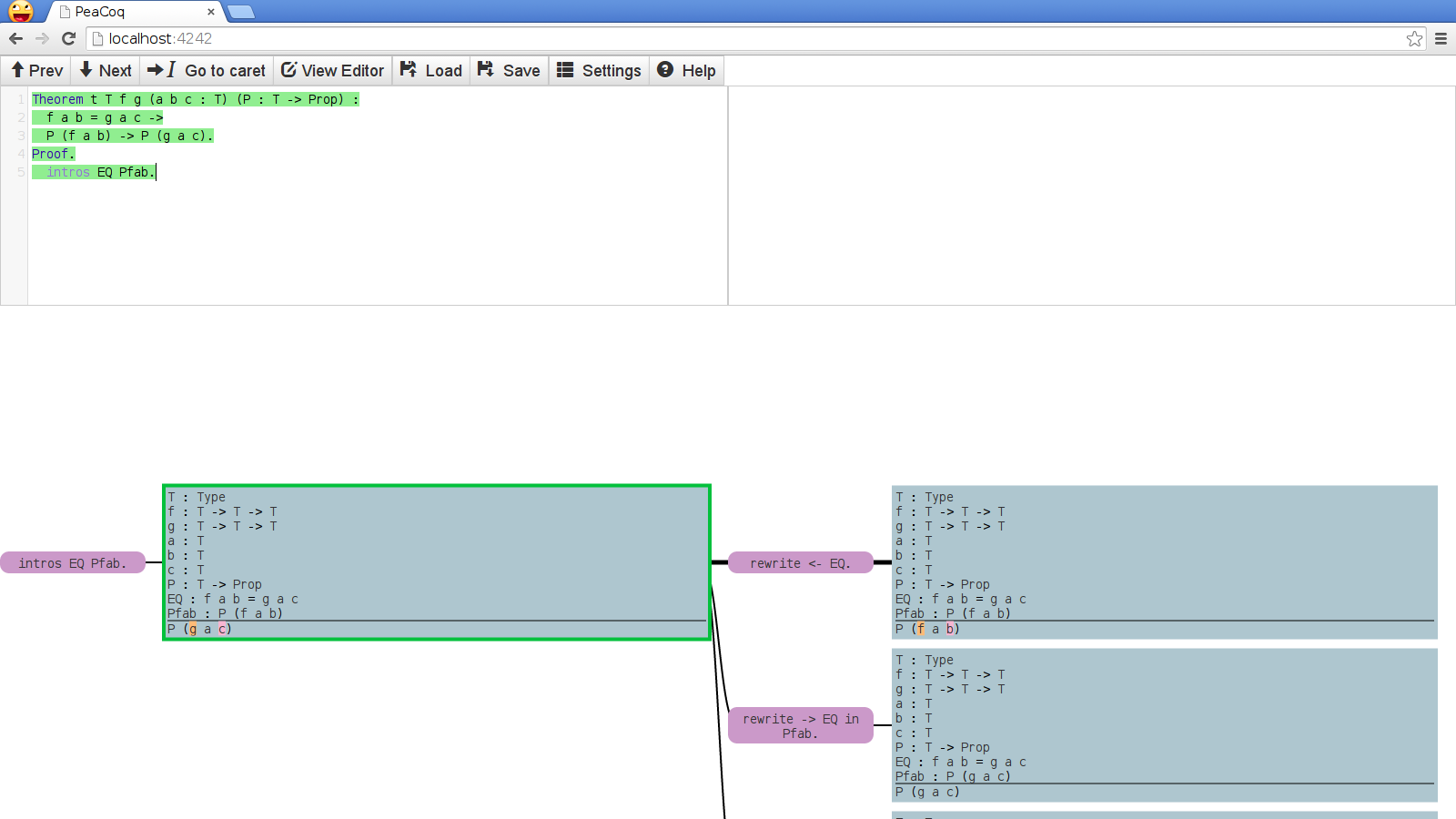
The main feature of PeaCoq is its tree mode. Whenever you enter a proof, the interface splits into this view:

The top part of the screen has your editor on the left, and a buffer for errors on the right. The bottom part shows your current proof context in the leftmost rectangle, a tactic in the purple node, and the resulting proof context in the right rectangle.

In the next sections, I will discuss two features of PeaCoq: the automated trial of tactics in the background, and the highlighting of the differences between proof contexts.

Automatically trying tactics

Like most programming languages, learning Coq requires making yourself familiar with a vernacular of syntactic elements and their proper grammar. In fact, Coq has three languages whose interaction is crucial to achieve anything:

• Vernacular, the language used to introduce constructs and change meta-level properties

• Gallina, the language used to define computational behaviors

• Ltac, the language used to interact with proof contexts.

Learning these three languages can be overwhelming. To bridge some of this “gap of execution”, PeaCoq can try tactics in the background, and display the results to the user. We only show the result of tactics that succeed and actually modify the context. This way, we avoid displaying tactics that may succeed yet do nothing, like firstorder.

The first challenge here is to pick a suitable set of tactics to try. Some tactics are benign to try all the time, while some tactics can take a very long time to succeed or fail. So far, we have only used a set of curated tactics, and try them in order of their expected complexity.

Now, most tactics have a plethora of arguments and variants that are sometimes useful, sometimes necessary to use in order to make progress. For instance, introduction tactics let you specify names or even deconstruction patterns. Rewrite tactics let you specify which occurence of the unified pattern to actually perform the rewrite on. Existential tactics need you to provide an existential witness. It is unclear how to cater for all of these. By default, PeaCoq will only try very simple things: it will not name introduced variables, it will try all rewrites in all directions for all names in local context, over all hypotheses and the goal. This quickly grows big, though in practice many of these tactics immediately fail.

Another problem is in displaying the succesful tactics. There usually are many succesful tactics, with often redundant results. In order to display sometimes dozens of goals, PeaCoq groups them in a two-dimensional fashion. So far, we group tactics by their purpose (introduction tactics, rewrite tactics, solvers, etc.).

Highlighting differences between proof contexts

Here the problem seems simple. Assuming you have parsed the proof context before and after running a tactic, I would like to identify a set of differences. These differences can be:

• the appearance or disappearance of a hypothesis
• the reordering of a hypothesis
• a set of structural changes within a hypothesis or the goal

where the last two may overlap. Here is an example of the visualization of such a changeset:

The red, shrinking streams indicate hypotheses that disappear. The blue stream indicates the repositioning of a hypothesis. The orange patches indicate changes in the structure of a term.

Computing the streams is not too difficult. The interesting part is in computing differences within terms.

There has been some research on computing differences between abstract syntax trees, mostly in order to highlight changes between versions of software. They are somewhat too complicated for our intent as they often also compute code movement.

The naïve approach here is to compute similarity top-down and highlight subnodes of the AST that differ. This is a good first approximation, but it may give some non-intuitive results. For instance, consider the simplification step from:

1

concat (cons n l) nil

to

1

cons n (concat l nil)

This algorithm would see that the top-level node is an application node on both sides, and would recursively highlight concat (cons n l) as being different from cons n, and nil as being different from (concat l nil) (remember, function application is left-associative). This is often confusing because the entire term looks different, and the fact that the application node is still an application node is somewhat insignificant. In these situations we want to lift the difference to the entire application.

This still leaves an issue. Consider the following:

Even though the algorithm is precise in identifying that only the function being applied and its second argument have changed, this diff is somewhat misleading as to the semantics of rewrite. It might be better to highlight the entire expression f a b as modified. I am currently toying with this idea, thinking of bubbling differences whenever a nested application has both a modified functional term and a modified argument. The bubbling could propagate all the way to the last modified argument. Of course, it would over-approximate cases where the tactic actually intended to modify only these two precise locations. I don’t know if this is often the case.

A last concern is the detection of generalization or instantiation of quantifiers. The current algorithm flags the entire term as different whenever the top-most node in the AST differs, which is unfortunate for quantifier instantiation when the resulting subgoal is a subterm of the original subgoal or vice-versa. Ideally, I would find the matching subtree, and somehow indicate visually that only the quantifier has disappeared.

Evaluating PeaCoq for novices

I have been trying to evaluate PeaCoq since January. During the winter quarter, Zachary Tatlock taught the graduate programming languages class at University of Washington using PeaCoq as the in-class editor and as an option for students.

Students were overall positive about PeaCoq, even though the version they use was very unstable and undergoing development while they were working with it. Some students chose not to use PeaCoq, either because they already had their own ProofGeneral setup, or because they had a bad experience with PeaCoq. At that time, the editor was primitive, the proof tree feature was very brittle, and it was impossible to switch in and out of the proof tree mode on the fly. Many of these problems are now solved!

While this was overall a positive experience, I felt I needed more conclusive evidence of the help provided by PeaCoq for beginners, so I set up an A-B study. I recruited 20 graduate students, randomly assigned pairs of them into one of two groups, and had them work through a one-hour lecture followed by a one-hour exercise session. Group A was to perform the exercises in a ProofGeneral setting, while group B used PeaCoq’s trees. Here is the averaged data per exercise.

As you can see, the data is fairly inconclusive, partly because of flaws of the study setup. Hours before the study started, I removed a lemma that made rev_distributes_over_concat easier to prove. Students in group A were extremely stuck, though two pairs found a solution that involved a sequence of five rewrites. Four out of five pairs in group B found that solution too. After a long period of time, we unlocked everyone.

Ignoring this exercise, we can notice a few things. In the first exercise, the control group was much faster than group B! It turns out, some groups got lost looking at all the options PeaCoq proposed, rather than trying things boldly. On the other hand, the control group had to try things without any preview, and therefore tried to apply the same technique as in the in-class exercises, which was exactly the right way to go.

Another issue that came up was the abundance of spurious options offered by PeaCoq. For instance, we introduced lemmas like:

1

Theorem concat_nil_right : forall l : natlist, concat l nil = l.

or

1

Theorem rev_involutive : forall l : natlist, rev (rev l) = l.

Therefore, upon mining for rewrite possibilities, PeaCoq would offer many spurious rewrites, like rewrite <- concat_nil_right., every time a list was in context. This tactic replaces l with concat l nil, which, while correct, is most often not something you would like (unless you wanted to put the goal in this shape to apply some lemma).

It would be nice to filter such options, either by indicating to PeaCoq that some rewrites are only helpful in one direction, or by having a smarter metric for complexity.

map'_unroll was very PeaCoq-friendly in that it was a goal that held by reflexivity while not looking reflexive, and would not simplify by simpl. PeaCoq users were immediately presented with a reflexivity. node, while most of the control group got stuck and asked me what to do.

The latter exercises were only reached by a few pairs of the control group within the allocated time (thus the null standard deviation).

Overall, while it seemed PeaCoq was very helpful in some places, there were many confounding factors and places were the options offered by PeaCoq were more overwhelming than helpful for novices.

I am working on alleviating some of these pitfalls, and hopefully another study will highlight the benefits of PeaCoq…

Other challenges and features

• Parsing Coq terms: Up to version 8.4, the protocol used in communicating with a coqtop process was fairly terrible. In particular, terms were exchanged as strings, which made the kind of techniques used to display term differences challenging. My current solution is equally unsatisfactory: I wrote a small parser for Coq’s syntax. It does not handle everything, in particular notations, and so fails to parse many terms. Upon failure, the diff feature takes the conservative approach of string comparison. Coq 8.5 seems to finally output ASTs, so hopefully PeaCoq could leverage this to avoid recomputing all this information!

• Generate robust proofs: ideally, I would like editor support to make my proofs more robust. One pitfall when using theorem provers is how boring it is to introduce names, but how practical they are to use to quickly refer to something. This makes for proofs scripts were names are automatically introduced, and are therefore very brittle to small changes. It would be nice if the editor could prevent one from using automatically-introduced names, or retroactively edit the proof to introduce the name “auto-manually” once it is used, by keeping track of where it appeared and when it is used!

• Reducing context clutter: consider the following screenshot, taken from somewhere within a proof in CompCert.

So many lines! In my experience, there is little value in having all those lines most of the time. In particular, I am often interested in hypotheses that have indexed types, and not so much in the others, that are just “data”. Here is what I envision instead for PeaCoq:

All the variables in context but whose type is of lesser interest have been removed. You should be able to access them somehow (maybe by hovering your mouse wherever they appear? maybe by some keyboard shortcut query? maybe they should still be visible in some folded pane?), but I don’t want them in my way most of the time. Of course there would be tricky interactions with the diff feature.

I would also like to be able to make hypotheses as “hidden” without necessarily hiding them in the proof script.

• Manipulating the structure of terms: Now consider this context.

This long unfolded term takes the entire screen space. I rarely need to see this unfolded version, and PeaCoq knows the structure of the term and has built a DOM object with the proper structure, I should be able to have this long term be folded, and only unfolded if I want to. I have not implemented this yet, but I would like it to look something like:

(Oops, there is a slight but in the stream algorithm!)

• Supporting Coq’s evolution: In general, it would be nice to stay up-to-date, in particular to support Coq’s new background processing mechanism. Now this would make for some non backwards-compatible changes, so I’d rather wait until the community switches to 8.5.

That’s all folks!

If you want to see or talk about PeaCoq, I will be attending PLDI in Portland next week! You can also find me as Ptival on #coq or email me!

The project lives on GitHub. Please report bugs or suggestions for enhancements! :)

While playing with Conor McBride’s material for his summer school on dependently-typed metaprogramming, I was puzzled as to how easy it was to implement matrix transposition. I will detail here what goes on, as I find the insight slightly amusing.

First, some boilerplate code:

module TraverseId where

open import Data.Nat
open import Function

We define standard length-indexed lists (usually named vectors), and related operations.

data Vec (X : Set) : ℕ → Set where
  ◇   :                         Vec X zero
  _,_ : {n : ℕ} → X → Vec X n → Vec X (suc n)

vec : ∀ {n X} → X → Vec X n
vec {zero}  x = ◇
vec {suc n} x = x , vec x

vapp : ∀ {n S T} → Vec (S → T) n → Vec S n → Vec T n
vapp ◇        ◇        = ◇
vapp (f , fs) (x , xs) = f x , vapp fs xs

We now define applicative functors, along with two instances for the identity functor and the fixed-sized vector functor (you can think of it as a finite tabulation).

record Applicative (F : Set → Set) : Set1 where
  infixl 2 _⟨⋆⟩_
  field
    pure  : ∀ {X} → X → F X
    _⟨⋆⟩_ : ∀ {S T} → F (S → T) → F S → F T
open Applicative {{...}} public

applicativeVec  : ∀ {n} → Applicative (λ X → Vec X n)
applicativeVec  = record { pure = vec; _⟨⋆⟩_ = vapp }

applicativeId : Applicative id
applicativeId = record { pure = id; _⟨⋆⟩_ = id }

We then proceed to define the traversable interface.

record Traversable (F : Set → Set) : Set1 where
  field
    traverse : ∀ {G S T}{{AG : Applicative G}} →
               (S → G T) → F S → G (F T)
open Traversable {{...}} public

You can try to think of traverse’s signature in these terms: given a G-effectful action transforming an element of S into an element of T, and a F-structure containing some elements of S, we can compute a G-effectful action building up a F-structure of elements of T. In some sense, we map the action into the structure, and then we fold the structure of actions into a structure of results.

Vectors of a given size are traversable:

traversableVec : {n : ℕ} → Traversable (λ X → Vec X n)
traversableVec = record { traverse = vtr } where
  vtr : ∀ {n G S T}{{_ : Applicative G}} →
               (S → G T) → Vec S n → G (Vec T n)
  vtr        f ◇         = pure ◇
  vtr {{aG}} f (s , ss)  = pure {{aG}} _,_ ⟨⋆⟩ f s ⟨⋆⟩ vtr f ss

The given exercise at this point in the course was to implement matrix transposition. It was heavily hinted that this would be implemented as a traversal, so I let myself be guided by the types, and write the following, where the question mark stands for a hole, a placeholder for a term that you do not want to write yet:

transpose : ∀ {m n X} → Vec (Vec X m) n → Vec (Vec X n) m
transpose = traverse ?

At that point, the type of the hole (the expected type of the term to be filled in place of the hole) was the following:

Goal: Vec .X .m → Vec .X .m

Well, do I have just the right candidate for that type! Even Agsy, the automated program search tool shipped with Agda, knows what to put in that hole!

transpose : ∀ {m n X} → Vec (Vec X m) n → Vec (Vec X n) m
transpose = traverse id

At that point though, the doubt builds in my mind. It seems to me that a traversal with the ineffectful identity function should just give me back the same structure I started with... Yet given the type of transpose, it definitely modifies the shape of the input structure. And at such a polymorphic type, with such a generic implementation, there’s only so much it can be doing! How does it work!?

Before trying to solve that question, I wonder whether I could implement the identity function as a matrix traversal... Again, being type-directed:

matrixId : ∀ {m n X} → Vec (Vec X m) n → Vec (Vec X m) n
matrixId = traverse ?

Can you guess the type of the hole? :-)

Goal: Vec .X .m → Vec .X .m

And indeed, here comes the implementation:

matrixId : ∀ {m n X} → Vec (Vec X m) n → Vec (Vec X m) n
matrixId = traverse id

Sounds familiar? Indeed, to implement matrix transposition and matrix identity, I wrote the exact same code! So something must be happening under the covers, at the level of implicit arguments.

Let’s play the part of the unification algorithm with our two toy functions. Recall the full polymorphic type of traverse:

traverse : ∀ {F : Set → Set}{G S T}{{AG : Applicative G}} →
                  (S → G T) → F S → G (F T)

So, by unification (the question-marked variables are now unification variables in scope):

-- by applying to id, ?S is unified with ?G ?T, therefore substituted
traverse id : (?G ?T → ?G ?T) → ?F (?G ?T) → ?G (?F ?T)

For our two examples, we ascribe the following type signatures:

-- transpose
traverse id : Vec (Vec X m) n → Vec (Vec X n) m

-- matrixId
traverse id : Vec (Vec X m) n → Vec (Vec X m) n

The following unification problems are to be solved:

-- transpose
?F ?S → ?G (?F ?T) ≙ Vec (Vec X m) n → Vec (Vec X n) m

-- matrixId
?F ?S → ?G (?F ?T) ≙ Vec (Vec X m) n → Vec (Vec X m) n

This gives rise to the following unification equations:

-- transpose
?F (?G ?T) ≙ Vec (Vec X m) n
?G (?F ?T) ≙ Vec (Vec X n) m

-- matrixId
?F (?G ?T) ≙ Vec (Vec X n) m
?G (?F ?T) ≙ Vec (Vec X n) m

And here are the potential solutions:

-- transpose
1: ?T = X ; ?F = λ S → Vec S n ; ?G = λ S → Vec S m

-- matrixId
1: ?T = X ; ?F = λ S → Vec (Vec S n) m ; ?G = id

2: ?T = X ; ?F = id ; ?G = λ S → Vec (Vec S n) m

However, another additional constraint, namely the implicit instance argument that requires ? G to be an applicative functor, prevents the second equation from being solved, as we did not provide a way for Agda to build nested instances.

The mystery is therefore solved: even though we wrote the same code, the implicit arguments have been inferred, type-directed by the unification, to be different. In the case of matrix transposition, the F-structure is the outermost vector layer, and the G-effect is the innermost vector layer. In the case of matrix identity, the entire matrix is the F-structure, and the G-effect is identity. It makes sense then, that traversing with no effect and the identity function preserves the matrix completely.

One may now wonder how come traversing a vector with a vector effect effectively transposes the entire structure, seen as a matrix. It is actually fairly simple once you start unfolding the definitions:

-- note that (1 , 2) stands for (1 , 2 , ◇), for simplicity and brevity
  traverse id ((1 , 2) , (3 , 4) , (5 , 6))
-- unfolding traverse for F = λ S → Vec S 3, that is unfolding traverseVec
= pure _,_ ⟨⋆⟩ id (1 , 2) ⟨⋆⟩ vtr id ((3 , 4) , (5 , 6))
-- repeatedly unfolding recursive calls to vtr
= pure _,_ ⟨⋆⟩ id (1 , 2) ⟨⋆⟩
  (pure _,_ ⟨⋆⟩ id (3 , 4) ⟨⋆⟩
  (pure _,_ ⟨⋆⟩ id (5 , 6) ⟨⋆⟩ pure ◇))
-- unfolding id...
= pure _,_ ⟨⋆⟩ (1 , 2) ⟨⋆⟩ (
  pure _,_ ⟨⋆⟩ (3 , 4) ⟨⋆⟩ (
  pure _,_ ⟨⋆⟩ (5 , 6) ⟨⋆⟩ pure ◇
  ))
-- unfolding pure, with the applicative instance for G = λ S → Vec S 2
= ((_,_) , (_,_)) ⟨⋆⟩ (1 , 2) ⟨⋆⟩ (((_,_) , (_,_)) ⟨⋆⟩ (3 , 4)
  ⟨⋆⟩ (((_,_) , (_,_)) ⟨⋆⟩ (5 , 6) ⟨⋆⟩ (◇ , ◇)))
-- the applicative application performs position-wise function application
= ((1 , _) , (2 , _)) ⟨⋆⟩ (((3 , _) , (4 , _)) ⟨⋆⟩ (((5 , _) , (6 , _)) ⟨⋆⟩ (◇ , ◇)))
= (1,_ , 2,_) ⟨⋆⟩ ((3 ,_ , 4 ,_) ⟨⋆⟩ ((5) , (6)))
= (1,_ , 2,_) ⟨⋆⟩ ((3 , 5) , (4 , 6))
= ((1 , 3 , 5) , (2 , 4 , 6))

All in all, matrix transposition is not implemented as a matrix traversal, but as a vector traversal with a column-building effect!

Finally, here is how it goes for matrix identity:

  traverse id ((1 , 2) , (3 , 4) , (5 , 6))
-- unfolding traverse for F = λ S → Vec (Vec S 2) 3, that is unfolding traverseVec
= pure _,_ ⟨⋆⟩ id (1 , 2) ⟨⋆⟩ vtr id ((3 , 4) , (5 , 6))
-- repeatedly unfolding recursive calls to vtr
= pure _,_ ⟨⋆⟩ id (1 , 2) ⟨⋆⟩
  (pure _,_ ⟨⋆⟩ id (3 , 4) ⟨⋆⟩
  (pure _,_ ⟨⋆⟩ id (5 , 6) ⟨⋆⟩ pure ◇))
-- unfolding id...
= pure _,_ ⟨⋆⟩ (1 , 2) ⟨⋆⟩ (
  pure _,_ ⟨⋆⟩ (3 , 4) ⟨⋆⟩ (
  pure _,_ ⟨⋆⟩ (5 , 6) ⟨⋆⟩ pure ◇
  ))
-- unfolding pure, with the applicative instance for G = id
= _,_ ⟨⋆⟩ (1 , 2) ⟨⋆⟩ (_,_ ⟨⋆⟩ (3 , 4) ⟨⋆⟩ (_,_ ⟨⋆⟩ (5 , 6) ⟨⋆⟩ ◇))
-- the applicative application performs just function application
= (1 , 2),_ ⟨⋆⟩ ((3 , 4),_ ⟨⋆⟩ (5 , 6))
= (1 , 2),_ ⟨⋆⟩ ((3 , 4) , (5 , 6))
= (1 , 2) , (3 , 4) , (5 , 6)